Well, this was an interesting, but frustrating, exercise. Don't bother reading any further, as the only one who might be interested in the following is Aerowhatt.
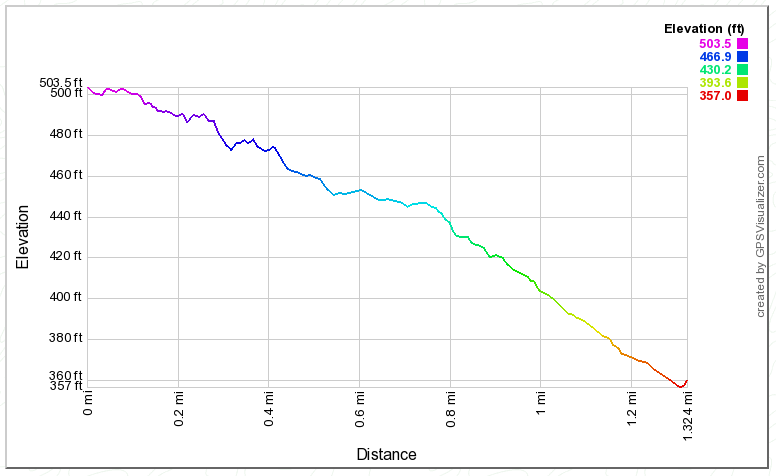
Here's the elevation chart of the road I take:
The
objective was to first get the car up to 35mph, kick it into
Neutral, and then coast all the way down. The idea was to repeat this with the car in
D (or
Eco or
B) and hold the accelerator steady to hold the 35 mph speed and then record the power consumption (ammeter reading). Simple, huh?
Here's what happens normally -
Looking at the above graph, it is fairly level for the first 0.1-mile with a fairly sharp curve so I use that distance to accelerate up to 35mph, kicking it into
Neutral at the 0.1-mile mark.
The car maintains a speed of 33mph-35mph for the distance from 0.1-mile to 0.8-mile, despite the road being somewhat curvy in places. In this mode, CaniOn reads 1.3A and instantaneous 8Wh/km. At the 0.8-mile mark the car starts accelerating and by the time it gets down to the 1.2-mile mark it is almost up to 40mph.
I realized why I never see that 40 mph in my everyday driving: at around the 0.9-mile mark (last curve followed by straight stretch) I reflexively drop it into D then Eco then B and consciously slow the car down using regen so that it is crawling by the time it hits the stop sign at the bottom (1.3mi). Also, that last stretch is occasionally a speed trap by the local sheriff (the speed limit is 30 mph), so by playing with regen I automatically avoid that issue. That's kinda my force-of-habit method of driving that road daily in the i-MiEV for the past five years.
Incidentally, with CaniOn, my figure of merit is to drop down my cumulative trip consumption to zero Wh/km by the time I hit that stop sign - it takes that long to counteract the sharp initial acceleration power draw, and the final regen really brings that number down fast.
So, what happened today when I tried it in
D -
What I decided to do was make a few runs in only that nice steady first portion of that drive: between 0.1 miles and 0.8 miles, and record the data using a voice recorder. In a nutshell, in my first few attempts today, trying to keep a steady foot on the accelerator in order to keep the speed in the 33mph-35mph range and then read the Amps on CaniOn
proved to be impossible. The Amps were all over the map, from a negative maybe 2A (slight regen) to a positive maybe 9A, as the car is operating in a very lightly-loaded region. The amps number was different every time I looked at it! I need to keep my foot from twitching or else I need a mechanical throttle with a vernier on it!
FWIW, it was our first very warm summer day today, afternoon temperature 87degF (30degC), battery was at 65%SoC, battery average temperature was 26degC (79degF) and RR=44 - just some meaningless data points.
On the drives
back up the hill I was better able to steady out the fluctuations, with perhaps an average of 25A at 35mph on that stretch between the 0.8mi and 0.1mi markers. Have to think about it, as that info might prove to be significant.
What does all this tell us?
Nothing! Over the next few days I will now see if I can develop a really gentle non-twitchy featherfoot to keep that accelerator pedal constant with the car at 35mph and then glance over at CaniOn for the amp reading, without worrying about deer jumping out in front of the car. To be continued...
Edit: I just had a duh! moment, as I forgot that I can upload the CaniOn data and can then dissect it. Also, I can take a screenshot of the CaniOn graph...